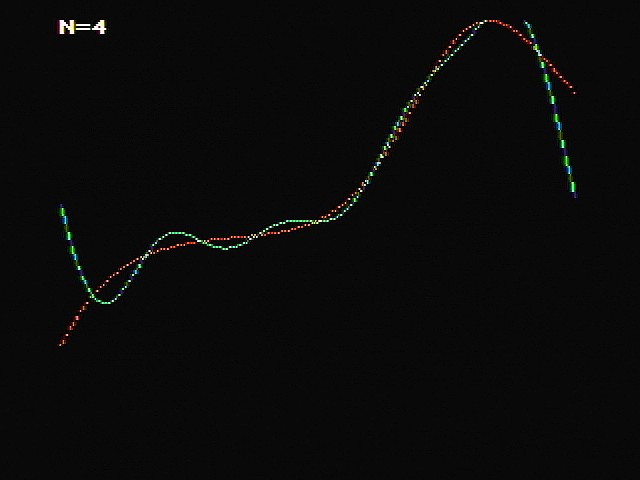
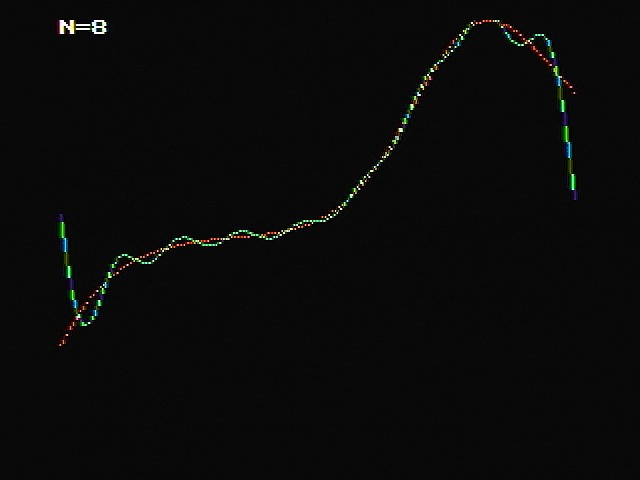
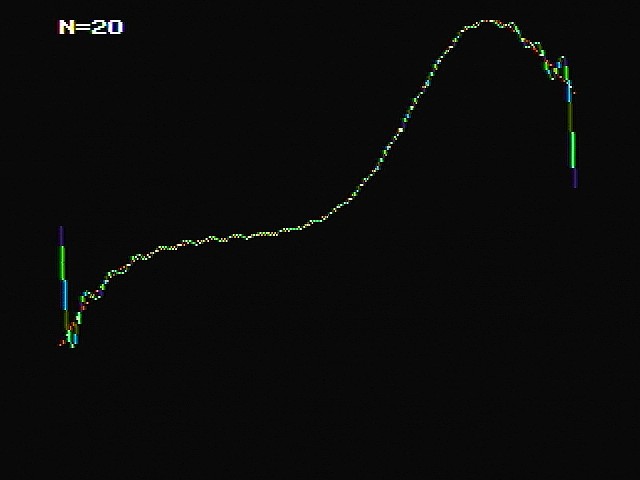
MachiKaniaでフーリエ級数の確認  投稿者：ケンケン  投稿日：2017年10月29日(日)16時44分3秒 NE0356lan1.rev.em-net.ne.jp 返信・引用
  MachiKania type Zで関数をフーリエ級数に展開するプログラム作成しました。
画像の赤いグラフが元の関数で、緑がフーリエ級数展開したものです。
元の関数はここではx*exp(sin(x))としています。

プログラムの最初に各種パラメータ設定しています。

D :定積分の分解能（関数の範囲を何分割するか）
N :級数を何回まで計算するか
T#:関数の範囲（-T#/2～+T#/2）

展開したい関数は、一番最後のLABEL FUNCのサブルーチン（関数）で定義しています。
書き換えて様々な関数を試すことができます。単純な数学関数だけでなく、引数から
条件指定することで矩形波なども作れます。

結果を見ると、Nを大きくすると元の関数に近づくのがよく分かります。

こんな風にMachiKaniaを数学の学習に使ってみるのはいかがでしょうか。

------------------------------------------------------------------------------
REM Fourier series

D=512:N=8:T#=2*PI#
DIM A#(N),B#(N)
USEGRAPHIC
H#=T#/FLOAT#(D)
GCOLOR 2
FOR I=-128 TO 127
  X#=FLOAT#(I)*T#/256
  GOSUB PLOT,I+128,GOSUB#(FUNC,X#)
NEXT
FOR I=0 TO N
  A#(I)=0:B#(I)=0
  FOR J=-D/2 TO D/2-1
   X#=FLOAT#(J)*H#
   A#(I)=A#(I)+GOSUB#(FUNC,X#)*COS#(FLOAT#(I)*X#)*H#
   B#(I)=B#(I)+GOSUB#(FUNC,X#)*SIN#(FLOAT#(I)*X#)*H#
  NEXT
  A#(I)=A#(I)*2/T#
  B#(I)=B#(I)*2/T#
  GPRINT 0,0,7,0,"N="+DEC$(I)
NEXT

GCOLOR 4
FOR I=-128 TO 127
  X#=FLOAT#(I)*T#/256
  Y#=A#(0)/2
  FOR J=1 TO N
   Y#=Y#+A#(J)*COS#(FLOAT#(J)*X#)+B#(J)*SIN#(FLOAT#(J)*X#)
  NEXT
  GOSUB PLOT,I+128,Y#
NEXT

WHILE INKEY()=0:WEND:END

LABEL PLOT
  IF ARGS(1)=0 THEN
   POINT ARGS(1),INT(-ARGS#(2)*20+100)
  ELSE
   LINE ,ARGS(1),INT(-ARGS#(2)*20+100)
  ENDIF
RETURN

LABEL FUNC
  VAR X#,Y#
  X#=ARGS#(1)
  Y#=X#*EXP#(SIN#(X#))
RETURN Y#